Symmetry scales guide

Scale types in Symmetry

Scales in Symmetry are set by choosing a scale type with the TYPE knob / CV input and selecting pitches with the pitch-unit buttons or with the RANDOM button / RAND CV input.

There are ten different scale types and all but the first one are symmetrical. The pitches in a symmetrical scale are evenly spread across its range and form the fundamental structure of the scale. The type of scale determines its range and number of fundamental pitches (also known as roots).

On top of this fundamental structure, identical sectional scales are built from each pitch of the symmetrical scale. In other words, each fundamental pitch of the symmetrical scale is the root of a sectional scale. The range of the sectional scale is determined by the interval between the fundamental pitches of the symmetrical scale.

Sectional scales are set with the pitch-unit buttons or with the RANDOM button / RAND CV input. Their structure and range are visualized with the pitch-unit button lights. Green color indicates that the pitch is selected, light off – the pitch is not selected, and faint green color indicates that the pitch is beyond the range of the sectional scale for the chosen scale type.

List of scale types in Symmetry

One root, one-octave range. This is the default scale type in Symmetry. It is ideal for creating the most widespread scales such as major, minor, all the modes, etc.

Two roots, one-octave range. This scale type divides the octave into two equal parts. For example, if we build this scale from C, then the second fundamental pitch (root) will be F#, and then the scale will repeat from C an octave above, etc. The same applies to the lower octaves. Sectional scales will be built from each root.

Three roots, one-octave range. The same principle applies here as well. Starting from C the roots are: C, E, Ab, and then C an octave above.

Four roots, one-octave range. Starting from C the roots are: C, Eb, F#, A, and then C an octave above.

Six roots, one-octave range. This scale type matches a whole-tone scale. Starting from C the roots are: C, D, E, F#, Ab, Bb, and then C an octave above.

Twelve roots, one-octave range. This scale type matches the chromatic scale. There are no sectional scales for it, as the interval between the roots is just one semitone and there is no space for more pitches in equal temperament. Starting from C the roots are: C, C#, D, Eb, E, F, F#, G, Ab, A, Bb, B, and then C an octave above.

Three roots, two-octave range. This scale type and the rest have ranges of more than one octave, i.e. they repeat at intervals greater than the octave. Starting from C the roots are: C, Ab, E, and then C two octaves above.

Four roots, three-octave range. Starting from C the roots are: C, A, F#, Eb, and then C three octaves above.

Six roots, five-octave range. Starting from C the roots are: C, Bb, Ab, F#, E, D, and then C five octaves above.

Twelve roots, eleven-octave range. This scale type goes beyond the range of human hearing. Nevertheless, it is an interesting scale type and has its applications. Starting from C the roots are: C, B, Bb, A, Ab, G, F#, F, E, Eb, D, Db, and then C eleven octaves above.

The chosen scale type along with a particular sectional scale form a complete symmetrical scale.

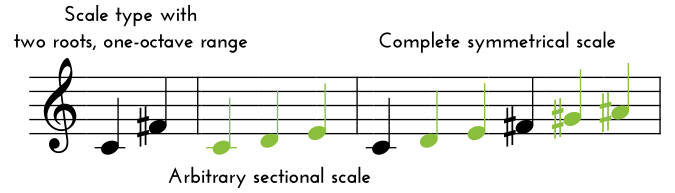
Tonal expansion and contraction of scales in Symmetry

Scales in Symmetry can be expanded or contracted with < and > buttons.

Scales with one-octave range can be expanded. When such a scale is expanded, the intervals between each scale degree are increased, while the pitch-units are preserved. This is achieved by rearranging the mutual positions of the pitch-units in the original scale. The number of expansions of a scale is determined by the number of pitch-units in that scale.

Scales with range of more than one octave can be contracted. When such a scale is contracted, the positions of its roots (and the corresponding sectional scales along with them) are rearranged so that they are as close as possible.

In both cases the CV outputs of Symmetry are translated accordingly.

Play with scale expansion and contraction to get a feel for them. Although they may sound complicated at first, they become easier to understand once you hear them in action. And they are very useful tools.

Happy music making!